Portfolio de Projet : Détection d'Anomalies avec Modèle Gaussien

1. Présentation du Projet

Ce projet, réalisé dans le cadre d'un cours en ligne de Stanford, implémente un algorithme de détection d'anomalies pour identifier des comportements anormaux dans des serveurs informatiques. L'approche utilise un modèle de distribution gaussienne pour détecter les points de données sortant le plus du lot, considérés comme des anomalies.

Dans ce contexte, nous travaillons avec un cas d'erreur binaire simple : normal ou anormal. Une distribution gaussienne suffit pour ce type de classification. Si nous avions plusieurs types d'anomalies à identifier, nous utiliserions un Gaussian Mixture Model (GMM), une méthode plus avancée de clustering permettant de gérer plusieurs distributions gaussiennes simultanément.

L'objectif est de démontrer comment implémenter un algorithme de détection d'anomalies compréhensible, explicatif et facile à implémenter, particulièrement efficace sur des données labellisées avec des cas d'erreur binaires.

Ces méthodes, fondées sur des modèles de distributions gaussiennes, permettent de détecter des cas non observés lors de l’entraînement en identifiant les points de données présentant une faible probabilité d’appartenance à la distribution normale, contrairement aux algorithmes de détection d’anomalies reposant sur des approches de classification supervisée.

2. Structure du Projet

a. Objectifs

• Implémenter l'algorithme de détection d'anomalies basé sur la distribution gaussienne
• Appliquer l'algorithme sur des données de serveurs (débit et latence)
• Trouver le seuil optimal pour la classification des anomalies via validation croisée
• Étendre la solution à un dataset haute dimension (11 features)

b. Dataset

Le projet utilise deux datasets fournis par Stanford :

• Dataset 2D : 307 exemples d'entraînement avec 2 features (débit en mb/s et latence en ms)
• Dataset haute dimension : 11 features capturant diverses propriétés des serveurs (charge CPU, utilisation mémoire, trafic réseau, etc.)
• Ensemble de validation : Données labellisées pour l'optimisation du seuil de détection

3. Implémentation de l'Algorithme

a. Estimation des Paramètres Gaussiens

Implémentation vectorisée de la fonction estimate_gaussian qui calcule la moyenne et la variance pour chaque feature :

• Moyenne : $$\mu_i = \frac{1}{m} \sum_{j=1}^{m} x_i^{(j)}$$
• Variance : $$\sigma_i^2 = \frac{1}{m} \sum_{j=1}^{m} \left(x_i^{(j)} - \mu_i\right)^2$$

Résultats sur le dataset 2D :

• Moyenne de chaque feature : [14.11222578, 14.99771051]
• Variance de chaque feature : [1.83263141, 1.70974533]

b. Fonction de Densité de Probabilité

Utilisation de la distribution gaussienne (univariée) pour calculer la probabilité de chaque point :

$$p(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$$

Les points dont la probabilité est inférieure au seuil ε sont classés comme anomalies.

c. Sélection du Seuil Optimal

Implémentation de select_threshold pour trouver le meilleur ε en utilisant le score F1 :

• Calcul des vrais positifs (tp), faux positifs (fp) et faux négatifs (fn)
• Précision : $$\text{prec} = \frac{tp}{tp + fp}$$
• Rappel : $$\text{rec} = \frac{tp}{tp + fn}$$
• Score F1 : $$F_1 = \frac{2 \cdot \text{prec} \cdot \text{rec}}{\text{prec} + \text{rec}}$$

4. Résultats et Visualisation

a. Dataset 2D

• Meilleur epsilon : 8.990853e-05
• Meilleur score F1 : 0.875 (87,5%)
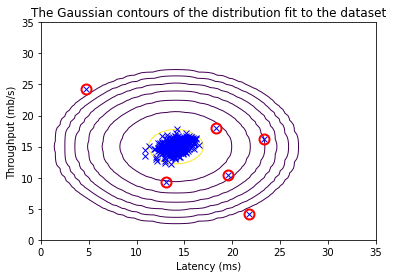
• Visualisation claire des contours de la distribution gaussienne
• Identification précise des anomalies (points encerclés en rouge)
• Les anomalies se situent dans les zones de faible probabilité

b. Dataset Haute Dimension

• Meilleur epsilon : 1.377229e-18
• Meilleur score F1 : 0.615385 (61,5%)
• Nombre d'anomalies détectées : 117 sur l'ensemble d'entraînement
• Le seuil beaucoup plus faible reflète la complexité accrue de l'espace à 11 dimensions

5. Analyse des Performances

a. Efficacité Algorithmique

• Complexité temporelle : O(m×n) pour l'estimation des paramètres, où m est le nombre d'exemples et n le nombre de features
• Performance : Algorithme très rapide et efficace, même avec peu de données
• Scalabilité : Passage du dataset 2D au dataset 11D sans problème de performance
• Simplicité : Implémentation directe sans complications techniques majeures

b. Comparaison des Résultats

Le score F1 plus élevé sur le dataset 2D (87,5%) comparé au dataset haute dimension (61,5%) s'explique par :

• La visualisation plus simple dans un espace 2D
• Moins de corrélations complexes entre les features
• La "malédiction de la dimensionalité" en haute dimension

6. Applications et Extensions

a. Cas d'Usage Concrets

• Monitoring de serveurs : Détection de pannes ou de comportements anormaux en temps réel
• Sécurité informatique : Identification d'activités suspectes ou d'intrusions
• Maintenance prédictive : Anticipation des défaillances matérielles

b. Expérience Professionnelle Connexe

Lors de mon stage de fin d'études avec Renault, j'ai appliqué des concepts similaires avec le Gaussian Mixture Model (GMM) pour un algorithme de clustering :

• Objectif : Créer des clusters de paniers de pièces liées aux accidents automobiles
• Méthodes comparées : K-Means, Agglomerative, Affinity Propagation, DBSCAN
• Résultat : GMM a obtenu les meilleurs résultats parmi toutes les méthodes testées
• Limites : Contraintes de temps n'ont pas permis de valider complètement l'approche sur d'autres cas et d'analyser en détail les clusters, mais la méthode GMM reste la plus encourageante

Cette expérience démontre l'applicabilité des modèles gaussiens dans des contextes industriels complexes.

7. Technologies Utilisées

• Méthodologie : Programmation vectorisée pour l'efficacité
• Temps d'entraînement : Environ 2-3 minutes

8. Perspectives d'Amélioration

• Algorithmes avancés : Exploration d'Isolation Forest, One-Class SVM ou Autoencoders pour des cas plus complexes
• Gaussian Mixture Model : Extension pour détecter plusieurs types d'anomalies simultanément
• Optimisation : Recherche en grille pour affiner les hyperparamètres
• Temps réel : Développement d'une interface de monitoring en temps réel
• Alerting : Intégration avec des systèmes de logging et d'alertes automatiques
• Features engineering : Analyse de corrélations et sélection de features pour améliorer les performances

9. Conclusion

Ce projet démontre l'efficacité d'une approche statistique simple pour la détection d'anomalies. Avec un score F1 de 87,5% sur le dataset 2D, l'algorithme gaussien prouve sa pertinence pour des cas d'usage réels où les données sont labellisées et les anomalies clairement définies.

La force de cette méthode réside dans sa simplicité d'implémentation, sa rapidité d'exécution et son caractère explicatif, permettant une compréhension intuitive des résultats. Cette approche constitue une excellente base pour des systèmes de monitoring et peut être étendue vers des modèles plus complexes comme le GMM pour des scénarios multi-classes.